前言

「函數式程式設計 (Functional Programming，簡稱 FP)」這個名詞應該大部分人都聽過，通常會看到類似這樣的定義：「FP 是一種使用純函數 (pure functions) 並避免副作用 (side effects) 的程式設計方法」。這聽起來十分抽象，而且「避免副作用」這件事在實務上真的可以做到嗎？

實際上，大部分的應用程式都必須產生副作用，甚至可以說副作用是我們使用軟體的根本原因。舉例來說，我們用 Email 應用程式就是為了要「寄信」、用電商網站就是要「把商品加入購物車並成立訂單」，這些與外部世界互動的行為，本質上都是副作用，但同時也是我們使用這些應用程式想達到的目的。如果要消滅副作用，那我不就不能寄信了嗎？想想就覺得沒有道理。

所以，副作用在 FP 中不是問題，消滅副作用也不是 FP 的目標。FP 的關鍵在於它提供了一套強大的工具與思維模型，來幫助我們管理因副作用而產生的程式碼複雜性。

範例：海鷗程式

為了更了解 FP 想解決的事情，我們先從一個海鷗程式碼開始。假設有一個鳥類觀察的應用，需要模擬海鷗鳥群的「增加 (addFlock)」與「繁殖 (multiplyFlock)」行為。如果是一個熟悉物件導向 (Object-Oriented Programming，簡稱 OOP) 的開發者，可能會寫出像下面這樣的 Flock class：

class Flock {
  constructor(n) {
    this.seagulls = n;
  }

  addFlock(other) {
    this.seagulls += other.seagulls;
    return this;
  }

  multiplyFlock(other) {
    this.seagulls = this.seagulls * other.seagulls;
    return this;
  }
}

這段程式中，addFlock 就是把另一個鳥群的數量加到自己身上，multiplyFlock 則是相乘。

現在假設有個比較複雜的情境：

const flockA = new Flock(5);
const flockB = new Flock(3);

const result = flockA
 .addFlock(flockB)
 .multiplyFlock(flockA)
 .seagulls;

console.log(result); // 顯示 64

程式印出的 result 是 64，但如果實際計算一下，會發現預期的結果應該是 (5 + 3) * 5，也就是 40 才對。那為何程式會算出錯誤的答案呢？
我們來看看程式碼的執行過程，問題的根源出在 addFlock 和 multiplyFlock 方法裡的這兩行：

this.seagulls += other.seagulls;

this.seagulls = this.seagulls * other.seagulls;

這兩行程式碼直接修改了物件內部的狀態。當 flockA.addFlock(flockB) 執行後，flockA 物件裡的 seagulls 已經從 5 變成了 8。因此當下一步 .multiplyFlock(flockA) 執行時，它計算的其實是 8 * 8，而不是我們預期的 8 * 5，最終導致了錯誤的結果。

可能會有熟悉 OOP 的開發者表示，這不是 OOP 的錯，是這段程式碼寫得不夠好，沒錯，這個範例並不是要批評物件導向，一個好的 OOP 程式設計師可能會有更好的方式來撰寫 Flock class，例如讓 addFlock 回傳一個新的 Flock 實例，而不是修改它自己。

這個舉例只是想凸顯程式設計中一個非常普遍且麻煩的問題：可變狀態 (mutable state)。當我們允許狀態在程式的各個角落被隨意修改時，程式碼的行為就變得難以追蹤和預測。而 FP 正好提供了一套強大的工具來處理這個挑戰。

函數式的解決方案

如果用函數式的風格來重寫，我們可以改寫為兩個函式：

const addFlock = (flockX, flockY) => flockX + flockY;
const multiplyFlock = (flockX, flockY) => flockX * flockY;

這兩個函式非常單純，它們接收輸入值，然後回傳一個新的值。它們絕對不會去修改任何傳入的鳥群。
現在用同樣的邏輯再計算一次剛剛的情境：

const flockA = 5;
const flockB = 3;

const result = multiplyFlock(
  addFlock(flockA, flockB),
  flockA
);

console.log(result); // 顯示 40

這次我們得到了正確答案 40。因為 flockA 和 flockB 的值從頭到尾都沒有被改變過。函式的輸出結果只跟輸入的參數有關，與它被呼叫的次數或順序無關，讓整個計算過程變得清楚且可預測。

所以 Functional Programming 是什麼?

上面範例所經歷的，正是 FP 的核心思想。在海鷗的範例中，那個導致 bug 的「修改外部狀態」的行為，就是我們所說的副作用。

副作用 (side effect) 是什麼?

程式設計中的副作用是指「除了傳回值以外的其他函數行為」，常見副作用例如：

• 寄電子郵件
• 修改全域變數
• 讀取檔案
• 發送網頁請求
• 存取系統狀態
• 插入資料至資料庫
• 輸出至螢幕 / 記錄日誌
• 查詢 DOM
• 獲取使用者輸入
• 修改檔案系統

補充一下，程式設計的副作用和醫學領域的「副作用」意義不同。醫學上說的副作用，例如吃感冒藥後會嗜睡，但這和程式設計中指的副作用意義不太相同。

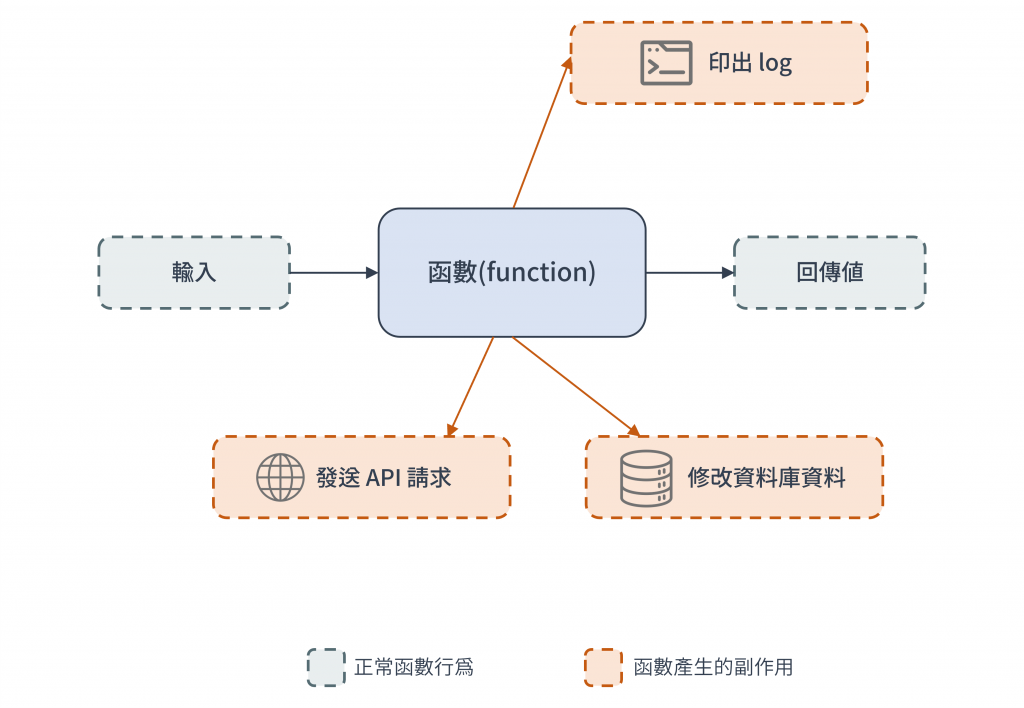
圖 1 程式設計中的副作用是指「除了傳回值以外的其他函數行為」(資料來源: 自行繪製)

那又為何 FP 要強調管理副作用呢？因為如果每次呼叫函數都會產生副作用，那可能會帶來一些程式設計師意料外的結果。就像我們剛剛遇到的，flockA 的狀態被意外修改，導致了 bug。為了避免這些意外，FP 的程式設計師會盡量將副作用與核心邏輯分離。

純函數 (pure functions) 是什麼?

而前面範例中修正了 bug、行為像數學一樣可預測的函式，就是純函數 (Pure Function)。一個函式如果滿足以下兩點，就是純函數 ：

1. 給定相同的輸入，永遠回傳相同的輸出。
2. 沒有任何可觀察的副作用。

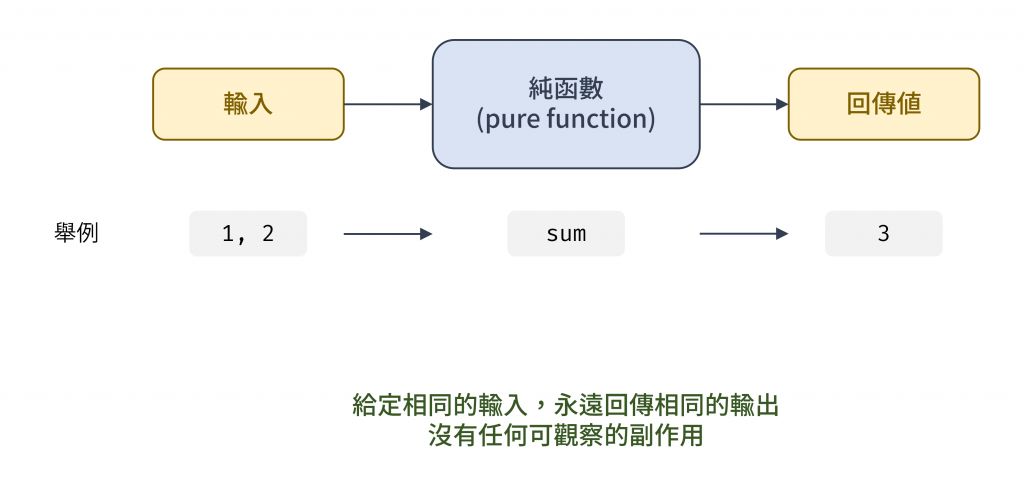
圖 2 純函數示意圖(資料來源: 自行繪製)

前面範例所提的 addFlock 和 multiplyFlock 函式就屬於純函數。它們具備可預測性、可測試性等優點。

Functional Programming 只能用純函數嗎?

在《簡約的軟體開發思維：用 Functional Programming 重構程式 - 以 Javascript 為例》書中有提到，人們常對 FP 有個誤解，就是為了避免副作用，FP 程式設計師只能使用純函數。但這想法有點誤會 FP，在 FP 的世界中一樣會有副作用和不純的函數，重點在如何管理它們帶來的意外結果。

Functional Programming 的意外超能力

當我們使用純函數時，還會得到一個意想不到的好處：我們的程式碼會變得像數學一樣，可以被推理和簡化。
再看一次剛剛的 addFlock 和 multiplyFlock，其實就是我們從小學就熟悉的加法 (add) 和乘法 (multiply) 。而它們也遵循著我們早已熟知的數學定律，例如：  

• 同一律(Identity)：add(x, 0) === x
• 分配律(Distributive)：multiply(x, add(y, z)) === add(multiply(x, y), multiply(x, z))

我們可以利用這些定律，來簡化一個稍微複雜的計算：

const flockA = 4;
const flockB = 2;
const flockC = 0;

// 原始計算
add(multiply(flockB, add(flockA, flockC)), multiply(flockA, flockB));

// 因為 flockC 是 0，根據「同一律」，add(flockA, flockC) 就等於 flockA
add(multiply(flockB, flockA), multiply(flockA, flockB));

// 根據「分配律」，這可以被重構成
multiply(flockB, add(flockA, flockA));

我們利用數學定律簡化了程式碼的邏輯，而這就是 FP 強大威力的一個縮影。當我們的程式碼由可預測的純函數構成時，我們就能獲得這種強大的推理能力，進而寫出更簡潔、更可靠的程式碼。

小結

所以，到底什麼是 functional programming？

與其記住複雜的學術定義，不如記住這個更務實的觀點：「FP 是一種專注於使用純函數來建構程式核心邏輯，並將難以預測的副作用嚴格管理與分離的程式設計範式。」

另外，此篇介紹許多 FP 帶來的好處，但這並不代表我們要完全拋棄物件導向。事實上，許多現代的框架和程式碼庫都巧妙地融合了兩者的優點。OOP 的優勢在於可以在複雜系統中看出單元跟單元間的互動，而 FP 則是用 immutable 的思維 (關於 immutable 會在之後文章介紹) 來撰寫程式，它用另一種視角來看待程式，幫助我們寫出更可靠、更易於維護的程式碼。

因此 OOP 和 FP 各有各的優點及適合應用的場景，實務上更常見兩者混搭的狀況。此系列文主要是想認識 FP 的思考方式，不等於完全否定 OOP 的實作價值。相關討論可參考為什麼要學 Functional Programming?此篇底下的討論，因為自己不算很熟悉 OOP，就不展開太多 OOP 與 FP 的優缺點比較了～